728x90
반응형
이미지 출처:https://namu.wiki/w/%ED%9E%99%20%ED%8A%B8%EB%A6%AC
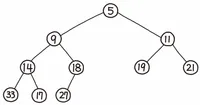
힙의 정의
우선 순위 큐를 이해하기 위해서는 힙이라는 것을 알아야 한다.
완전 이진트리의 일종으로 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안되었다.
힙의 특징
키 값의 대소관계는 오로지 부모 노드와 자식노드 간에만 성립하여 형제 사이에는 대소 관계가
정해지지 않는다.
(예를 들어 9와 14사이에는 우선순위가 있지만 14와 18사이에는 우선순위가 존재하지 않는다.)
힙의 시간 복잡도는 O(logn)이다.
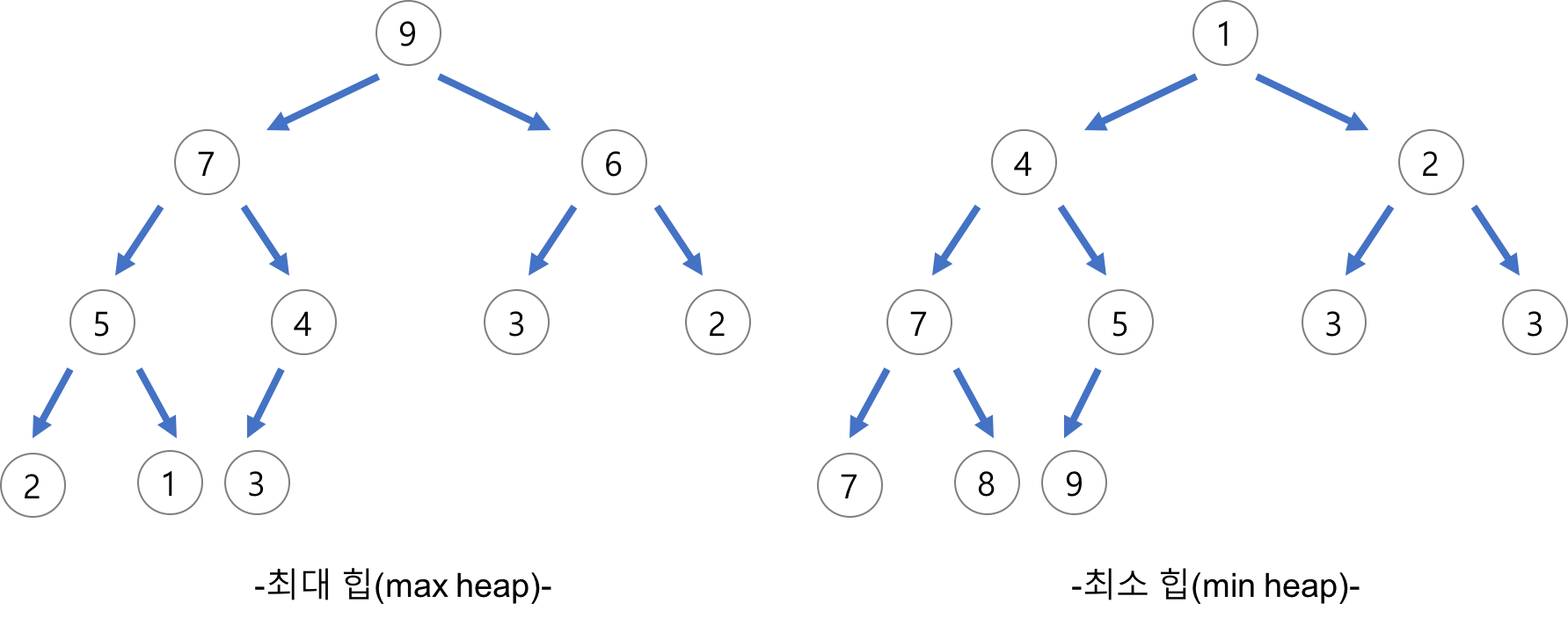
힙의 종류
- 최대 힙(Max Heap): (완전 이진 트리) + (부모 노드 > 자식 노드)
- 최소 힙(Min Heap): (완전 이진 트리) + (부모 노드 < 자식 노드)
이미지 출처:https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html
힙 구현 시 함수의 종류
Priority_Queue* HeapInit() -> 힙의 초기화를 해준다.
bool HIsEMpty() -> 힙의 enpty여부를 확인한다.
int GetParentIDx(int id) ->부모 인덱스를 반환한다.
int GetLchild(int id) -> 왼쪽 자식 인덱스를 반환한다.
int GetRchild(int id) -> 오른쪽 자식 인덱스를 반환한다.
int GetHichild(int id) -> 더 큰 자식 인덱스를 반환한다.
void HInsert(char data, int prt) -> 우선 순위와 데이터를 저장한다.
char HDelete() -> 가장 높은 우선순위 데이터를 삭제한다.
힙 구현 전 설명
배열의 첫 번째 인덱스는 1로 0은 구현 상 사용하지 않는다.
힙에서의 부모 노드와 자식 노드의 관계
- 왼쪽 자식의 인덱스 = (부모의 인덱스) * 2
- 오른쪽 자식의 인덱스 = (부모의 인덱스) * 2 + 1
- 부모의 인덱스 = (자식의 인덱스) / 2
최소힙을 기준으로 삽입과 삭제를 설명해 보겠다.
힙의 삽입
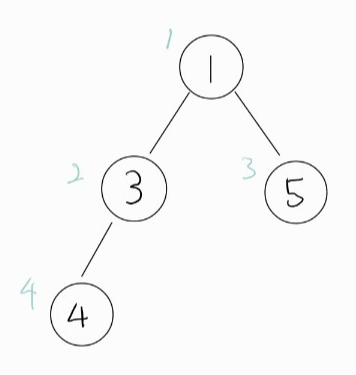
- 다음 배열에서 우선순위 2의 노드 삽입을 진행하겠다.

- 2가 더 우선 순위가 높으므로 부모 노드와 바꾸어 준다.
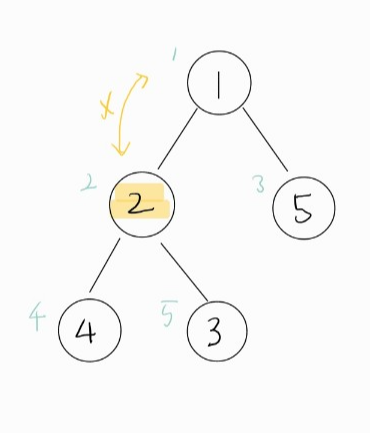
- 1이 더 우선 순위가 높으므로 부모 노드와 바꿀 수 없어 그대로 종료한다.
힙의 삭제

- 1우선 순위 노드를 먼저 제거해 준다.
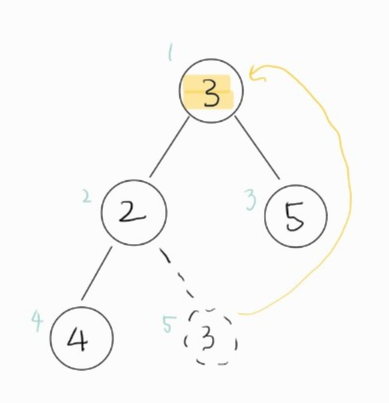
- 끝에 있는 노드를 1인덱스 위치로 옮겨준다.

- 2가 더 우선 순위가 높으므로 자식 노드와 바꿔준다.

- 3이 더 우선 순위가 높으므로 더 이상 바꾸지 않고 종료한다.
힙의 구현
#include <iostream>
#include <vector>
using namespace std;
class Heap {
private:
struct HeapElem {
int pr;
char data;
};
struct Priority_Queue {
int count;
HeapElem heaparr[100];
};
public:
Priority_Queue* arr;
Heap() {
arr = HeapInit();
}
Priority_Queue* HeapInit() {
Priority_Queue* newArr = new Priority_Queue;
newArr->count = 0;
newArr->heaparr;
return newArr;
}
bool HIsEMpty() {
if (this->arr->count == 0) {
return true;
}
else {
return false;
}
}
int GetParentIDx(int id) {
return id / 2;
}
int GetLchild(int id) {
return id * 2;
}
int GetRchild(int id) {
return id * 2 + 1;
}
int GetHichild(int id) {
if (arr->heaparr[GetLchild(id)].pr < arr->heaparr[GetRchild(id)].pr)
return GetLchild(id);
else
return GetRchild(id);
}
void HInsert(char data, int prt) { //우선 순위에 맞게 저장
HeapElem newNode = {prt, data}; //노드에 저장해놓는다.
int idx = (arr->count) + 1;
while (idx != 1) { //최상위 인덱스가 나올때까지 반복한다.
if (newNode.pr < arr->heaparr[GetParentIDx(idx)].pr) {
arr->heaparr[idx] = arr->heaparr[GetParentIDx(idx)];
idx = GetParentIDx(idx);
}
else {
break;
}
}
arr->heaparr[idx] = newNode;
(arr->count)++;
}
char HDelete() { //가장 높은 우선순위 데이터 삭제
char del = arr->heaparr[1].data;
arr->heaparr[1] = arr->heaparr[arr->count];
(arr->count)--;
int parentidx = 1, childidx = 1;
while (parentidx != arr->count) {
if (arr->heaparr[parentidx].pr > arr->heaparr[GetHichild(parentidx)].pr) {
childidx = GetHichild(parentidx); //미리 저장을 해놓아야 한다.
HeapElem tmp = arr->heaparr[parentidx];
arr->heaparr[parentidx] = arr->heaparr[GetHichild(parentidx)];
arr->heaparr[GetHichild(parentidx)] = tmp;
parentidx = childidx; //아래로 옮겨준다. parentidx =GetHichild(parentidx); 하면안된다. (이미 바뀐 뒤이기 때문)
}
else
break;
}
return del; //삭제한 값 반환
}
};
int main() {
int i;
Heap queue;
queue.HInsert('A', 2);
queue.HInsert('B', 1);
queue.HInsert('C', 3);
queue.HInsert('D', 5);
queue.HInsert('E', 4);
cout << queue.HDelete() << "\n";
cout << queue.HDelete() << "\n";
cout << queue.HDelete() << "\n";
cout << queue.HDelete() << "\n";
cout << queue.HDelete() << "\n";
}
다음은 힙을 이용하여 우선순위 큐를 만들어 구현해보겠습니다..
반응형
'알고리즘' 카테고리의 다른 글
| [정렬 알고리즘] 버블, 선택, 삽입 정렬 c++ 구현 (1) | 2024.02.27 |
|---|---|
| [Union find] c++ 구현 및 설명 (0) | 2024.02.22 |
| [DP] 동적 계획법 알고리즘 c++ 설명 (0) | 2024.02.10 |
| [이진트리] map, set c++ 구현 (0) | 2024.02.09 |
| [이진트리] 기본 c++구현 및 이진 트리 순회 설명(전위,중위,후위) (0) | 2024.02.09 |



